Typing the Technical Interview in TypeScript
this blogpost shows how to implement FizzBuzz in TypeScript using types only — with no runtime code whatsoever. The full solution can be viewed interactively in this TypeScript playground. This blogpost shows how it's done, step by step.
“Here’s a simple coding task,” the interviewer says — “You can use any language you want.” they said with confidence. "Any language?" I smirked.
The problem is called FizzBuzz, and the rules are the following:
For any given number, print the numbers from 1 until the given number, while:
- For any number which is divisable by 3, print "Fizz"
- For any number which is divisable by 5, print "Buzz"
- For any number which is divisable by 15, print "FizzBuzz"
- Otherwise, print the number as it is
For example, FizzBuzz of 16 would be:
1, 2, Fizz, 4, Buzz, Fizz, 7, 8, Fizz, Buzz, 11, Fizz, 13, 14, FizzBuzz, 16
A simple JavaScript code that does it would be something like:
function fizzbuzz(n) {
for (let i = 1; i <= n; i++) {
if (i % 15 === 0) {
console.log("FizzBuzz");
} else if (i % 3 === 0) {
console.log("Fizz");
} else if (i % 5 === 0) {
console.log("Buzz");
} else {
console.log(i);
}
}
}
But... isn't it too obvious?
Going Head Deep into Types
Apparentally, TypeScript is a Turing-complete language. And I'm not talking about the fact that it compiles into JavaScript and JavaScript is a turing complete language. TypeScript's type system is in fact turing complete!. So by using some computer science and TypeScript hackery, we can solve most problems without compiling them to JavaScript altogether.
Yes, that's true. So let's do it — launch a new TypeScript playground and start typing!
The first thing we need to do is have some confidence that what we write is true and we don't have bugs. So let's write a very simplistic test framework:
type Eq<A, B extends A> = "passes";
The Eq<A, B> type can ensure that B ⊆ A, or in English: B is a subset or equal to A. In our case, we will refer to this as if it means B = A, because we don't use any sets here, only concrete values. Here's an example:
type test_eq = [
Eq<"Hello", "Hello">, // passes
Eq<"Hello", "world">, // fails with "'world' does not satisfy constraint 'Hello'"
];
The next thing is dealing with numbers. At the time of writing, TypeScript's only notion of numbers is the number. This is not good enough for us:
- We don't support negative numbers
- We need to do math operations on compile time
Since TypeScript doesn't give us these constructs, let's make our own representation of numbers:
type NAN = "invalid number"; // we don't support negative numbers
type _0 = 0; // a type literal
Now that we have _0 which is 0, how do we get 1? We'll have our own implementation of how numbers look like — we'll declare them as the following:
type Increment<N> = [N, "+1"];
type _1 = Increment<_0>; // [0, "+1"]
type _2 = Increment<_1>; // [[0, "+1"], "+1]
// type _3 = ...
// I have added more numbers but truncated
This isn't as easy as writing 1 and 2, but it gives us the ability to increment numbers with unlimited range. By the end of this post, we'll change it so our program will work only on a specific range of numbers, but will use real numbers and not our representation. However, all the math we're going to do next will work on both formats!
Now that we can get to any number we want, the next thing we want to have is "IsDivisableBy". This will take us some time to get there because we don't have any math operations other than increment. We'll need to implement Decrement<N> and Subtract<N, Amount> before getting to division.
So how would we implement Decrement<N>?
TypeScript has a feature called "Conditional Types". It basically provides the ability to write code in the format of A extends B ? C : D. We'll again assume extends means equals. Another feature that the conditional types provide is the keyword infer, which can be in any part of the type we compare against: A extends Promise<infer B> ? B : unknown will return the inner type of a Promise if A is a promise, or unknown if it isn't.
type Decrement<N> = N extends Increment<infer D> // If N is some number that was incremented
? D // return the number that was incremented
: NAN; // otherwise, return NAN because _0 wasn't incremented and -1 is not in our range!
type test_decrement = [
Eq<Decrement<_1>, _0>,
Eq<Decrement<Decrement<_1>>, NAN>,
Eq<Decrement<Decrement<_2>>, _0>,
];
Implementing Decrement<N> wasn't straightforward, but after learning the trick it makes a lot of sense. Next up, is implementing Subtract<N, Amount>. This is where it gets a little trickier.
TypeScript's type system has no notion of loops, but we can do recursion. It's good, because implementing subtract as recursion is not very hard. Here's an implementation in plain JS:
function subtract(n, amount) {
if (amount === 0) {
return n;
} else {
return subtract(decrement(n), decrement(amount));
}
}
Translating to TypeScript types seems kinda intuitive with conditional types:
type Subtract<N, Amount> = Amount extends _0
? N
: Subtract<Decrement<N>, Decrement<Amount>>;
Unfortunately, TypeScript does not support recursive type aliases at this time of writing, so it errors with a message like Subtract circularly references itself. Fortunately, it can be avoided by using some tricks. It is recommended not to do that in your production apps, but solving a puzzle is for plain fun. So we'll do it anyway!
A nice trick to hack around it is to use an object where the keys are your stop conditionals, and then immediately reading a specific key based on the conditional. Hard to grasp, but let's see it in action:
type Subtract<N, Amount> = {
amount_is_zero: N;
recurse: Subtract<Decrement<N>, Decrement<Amount>>;
}[Amount extends _0 ? "amount_is_zero" : "recurse"];
type test_sub = [
Eq<Subtract<_2, _1>, _1>,
Eq<Subtract<_2, _2>, _0>,
Eq<Subtract<_2, _0>, _2>,
Eq<Subtract<_1, _2>, NAN>,
];
Now that we have Subtract<N, Amount>, we can check if a number is divisable by another! The "algorithm" for finding if a number A is a multiple of another one B is fairly simple:
function is_divisable_by(a, b) {
if (a === 0) return true;
if (a < 0) return false;
return is_divisable_by(subtract(a, b), b);
}
Let's see it in action for A=9, B=3
A: 9 B: 3 9 > 0 => 9 - 3 = 6 6 > 0 => 6 - 3 = 3 3 > 0 => 3 - 3 = 0 0 == 0 => true
And for A=10, B=3
A: 10 B: 3 10 > 0 => 10 - 3 = 7 7 > 0 => 7 - 3 = 4 4 > 0 => 4 - 3 = 1 1 > 0 => 1 - 3 = -2 -1 < 0 => false
Let's put it into types:
type IsDivisableBy<A, B> = {
a_eq_0: true;
a_lt_0: false;
recurse: IsDivisableBy<Subtract<A, B>, B>;
}[A extends NAN ? "a_lt_0" : A extends _0 ? "a_eq_0" : "recurse"];
type test_divisable_by = [
Eq<IsDivisableBy<_4, _2>, true>,
Eq<IsDivisableBy<_3, _2>, false>,
Eq<IsDivisableBy<_5, _3>, false>,
Eq<IsDivisableBy<_6, _3>, true>,
];
Now we can make a nice type aliases for our convenience:
type IsDivisableBy3<N> = IsDivisableBy<N, _3>;
type IsDivisableBy5<N> = IsDivisableBy<N, _5>;
We can also add IsDivisableBy15. A number is divisable by 15 if it divides by 3 and 5. How about we use our IsDivisableBy3<N> and IsDivisableBy5<N> types?
For that, we need to implement the And<A, B> type, which will work like && in JavaScript, but in compile time:
type And<A, B> = A extends true ? (B extends true ? true : false) : false;
type IsDivisableBy15<N> = And<IsDivisableBy3<N>, IsDivisableBy5<N>>;
Getting a FizzBuzz solution for one element
Warning: the following code is going to be ugly.
We are going to write FizzBuzzNth<N> that will get a number N and will return "Fizz" if it is divisable by 3, "Buzz" if it is divisable by 5, "FizzBuzz" if by 15, otherwise the number N:
type FizzBuzzNth<N> = IsDivisableBy15<N> extends true
? "FizzBuzz"
: IsDivisableBy3<N> extends true
? "Fizz"
: IsDivisableBy5<N> extends true
? "Buzz"
: N;
type test_fizzbuzznth = [
Eq<FizzBuzzNth<_1>, _1>,
Eq<FizzBuzzNth<_2>, _2>,
Eq<FizzBuzzNth<_3>, "Fizz">,
Eq<FizzBuzzNth<_4>, _4>,
Eq<FizzBuzzNth<_5>, "Buzz">,
Eq<FizzBuzzNth<_6>, "Fizz">,
Eq<FizzBuzzNth<_14>, _14>,
Eq<FizzBuzzNth<_15>, "FizzBuzz">,
Eq<FizzBuzzNth<_16>, _16>,
];
Now the only thing left is to construct a list with all the results.
Collecting the results
TypeScript type system has no array functions. But we can imitate the array functions using some utilities in TS that might help here. Let's implement the Unshift<Element, List> type, that adds Element to the beginning of List:
type Unshift<Element, List extends Array<any>> = Parameters<
(e: Element, ...list: List) => any
>;
type test_unshift = [
Eq<Unshift<1, []>, [1]>,
Eq<Unshift<2, [1]>, [2, 1]>,
Eq<Unshift<"hello", [2, 1]>, ["hello", 2, 1]>,
];
Waaaaaait what?! We use the Parameters<Fn> utility type to get an inline function's parameters. This is a nice and easy way to prepend a value to a list in TypeScript. Hackery, I told you.
Now let's create the FizzBuzzUpTo<N> type. What are we going to do here? We're going to do a recursion until N reaches _0. We will construct a list with the results of FizzBuzzNth<N> for each N and we will prepend it to our list.
For that, we need to have another generic argument, we'll call Output which will be... the output. It should have a default value of an empty list, so we won't need to provide it when we're using FizzBuzzUpTo<N>.
We'll start with some N, and after the first iteration we'll get something that looks like:
FizzBuzzNth<Decrement<N>, [FizzBuzzNth<N>]>;
Keep in mind that we start with the biggest number, and we decrement it on every iteration adding the values to the left of the list, so it'll be something like
[FizzBuzzNth<N-2>, FizzBuzzNth<N-1>, FizzBuzzNth<N>];
How would we implement it as a type?
type FizzBuzzUpTo<N, Output extends any[] = []> = {
output: Output;
recurse: FizzBuzzUpTo<Decrement<N>, Unshift<FizzBuzzNth<N>, Output>>;
}[N extends _0 ? "output" : "recurse"];
// prettier-ignore
type test_fizzbuzzupto = [
Eq<
FizzBuzzUpTo<_16>,
[
_1, _2, "Fizz", _4, "Buzz", "Fizz", _7, _8,
"Fizz", "Buzz", _11, "Fizz", _13, _14, "FizzBuzz", _16
]
>
];
Woohoo! We have FizzBuzz working!
Extending it to real numbers
If you'll take a look at the numbers, you'll see that they still use our own representation. The interviewer (which we have might already forgot about them because we were so into the code) wouldn't be happy to see this. They are used to their version of numbers which might and might not be nicer than ours.
I told you earlier that we can use real numbers but it'll force ourselves to have a limited range. Let's do it. Comment out the Increment<N> and Decrement<N> and paste the following implementation:
// prettier-ignore
type Increment<N> = [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20][Extract<N, number>];
// prettier-ignore
type Decrement<N> = [NAN,0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20][Extract<N, number>];
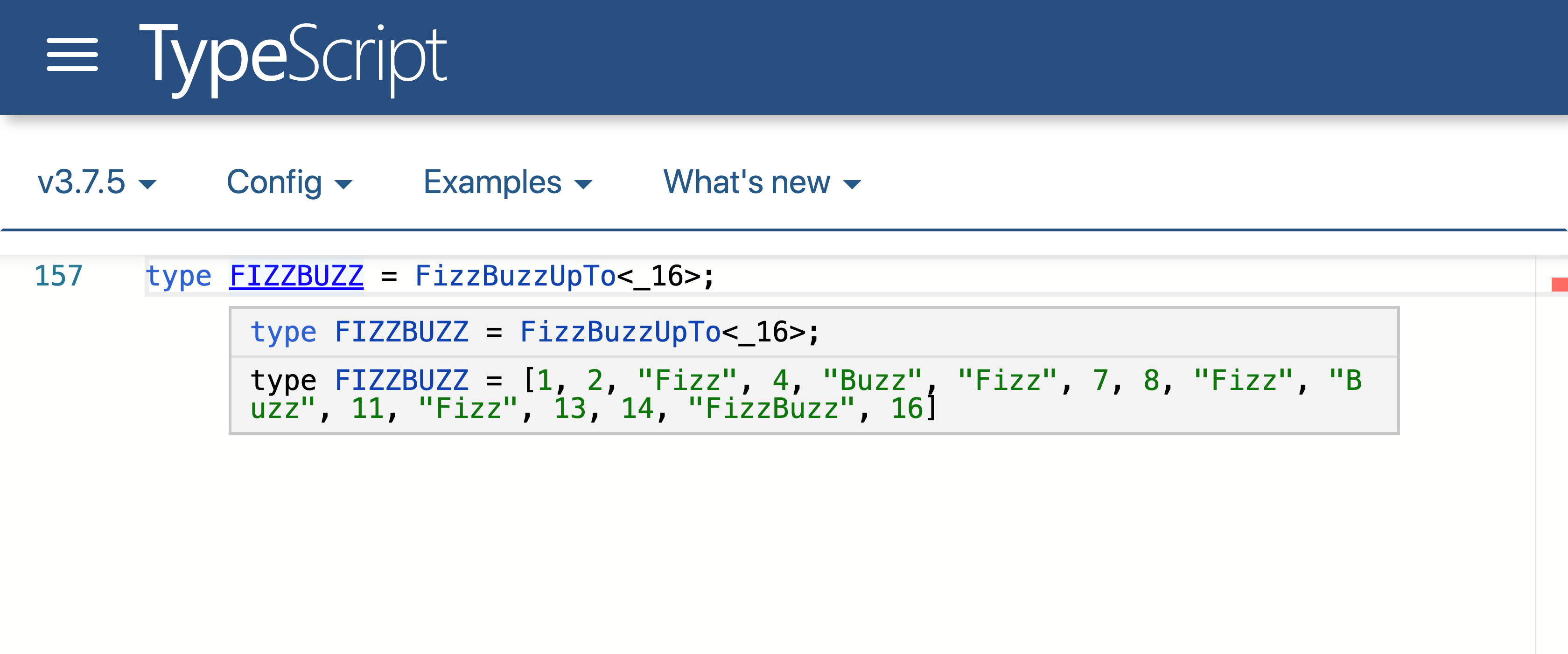
type FIZZBUZZ = FizzBuzzUpTo<_16>;
Imagine Extract<A, B> is a way to cast A as B. Our implementation of Increment<N> is basically a zero-indexed list of numbers — on index 0 we get 1, index 1 gets us 2. This is an easy way to implement incrementation. Decrement<N> is using the same trick. index 0 returns NAN which a implies negative number, index 1 returns 0, index 2 returns 1, etc.
 FIZZBUZZ
FIZZBUZZ
Now, we have a fully working FizzBuzz solution, with no runtime involved. I hope the recruiter is happy and I'll get the job.
Will update.